
Keywords 2H 3-j Symbol 4He 9-j Symbol 18O 19F 20Ne alpha analyzing power ANC angular angular momentum Bessel function Binding Energy charge Clebsch-Gordon Coulomb Coulomb Energy Cross section decay deformation degree of freedom denoising density matrix deuteron diagonalization dimension DNP Eigen System electromagnetism electron Fourier transform frame frequency GEANT4 Glauber Model gyromagnetic half life Hankel Hartree-Fock HELIOS helium hydrogen hypergeometric impedance isospin Laguerre Laplacian Larmor Lorentzain Magnetic magneton Microwave moment momentum natural unit neutron Nilsson orbital NMR p2p paper reading perturbation phase shift Planck Pol. Bohrs model of hydrogen is based on the nonclassical assumption that electrons travel in specific shells, or orbits, around the nucleus. and apply the DOWN operator, we can fins out all, and the normalization constant is easy to find by the normalization condition in spherical coordinate, the normalization factor is, instead of 1 in rectangular coordinate. Since there is no more higher z-component.īy solve this equation, we can find out the exact form of and sub this in to L 2, we can know. as we know, The z component of the a VECTOR must have some maximum. It is truly easy to find out the exact form of the by using the ladder operator. Which means, the UP operator is increase the z-component by 1, the constant there does not brother us. If we denote the angular momentum as L, and the z component of it is Lz, thus we have,Īs every quadratic operator, there are “ladder” operator for “up” and “down”. the radial part is not so trivial, but the angular part is so easy. Thus the solution of the “wave function” of the electron, which is also the probability distribution of the electron location, contains 2 parts as well. The angular part can be so simple that it is the Spherical harmonic. by that mean, the momentum operator (any one don’t know what is OPERATOR, the simplest explanation is : it is a function of function.) automatically separated into 2 parts : radial and angular part. that is better and easy for calculation because the coulomb potential is spherical symmetric. we put the Coulomb potential in the Schrödinger equation, change the coordinate to spherical. like Feynman, Dirac, Landau, Pauli, etc… OK, lets check how easy it is.Īnyway, we follow the usual say in every text book. Moreover, many famous physicists said it is easy. Why i suddenly do that is because, many text books said it is easy to calculate the energy level and spectrum for it. the fact is, there is no “trajectory” or locus for the electron, so technically, it is hard to say it is moving! almost center, and an electron moving around. it only contains a proton at the center, um. The interesting thing is about the energy level of Hydrogen atom. In the Bohr model of the hydrogen atom, what is the de-Broglie wavelength for the electron when it is in(a) the ( n1 ) level(b) the ( n4 ) level In e. and understand the concept of hydrogen is very helpful to understand the nuclear, because many ideas in nuclear physics are borrow from it, like “shell”. But that is what i were learning and learned.

#HYDROGEN BOHR MODEL FREE#
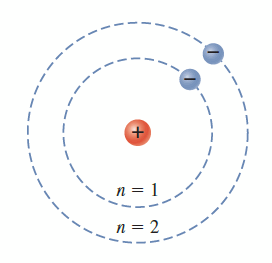
The electron in an atom is more stable than a free electron.OK, here is a little off track. It corresponds to an ionised atom where the electron and the nucleus are infinitely separated. It is the maximum energy that an electron can possess in an atom. These shells are numbered as one, two, three, four or termed as \(\rm \), the energy becomes zero.
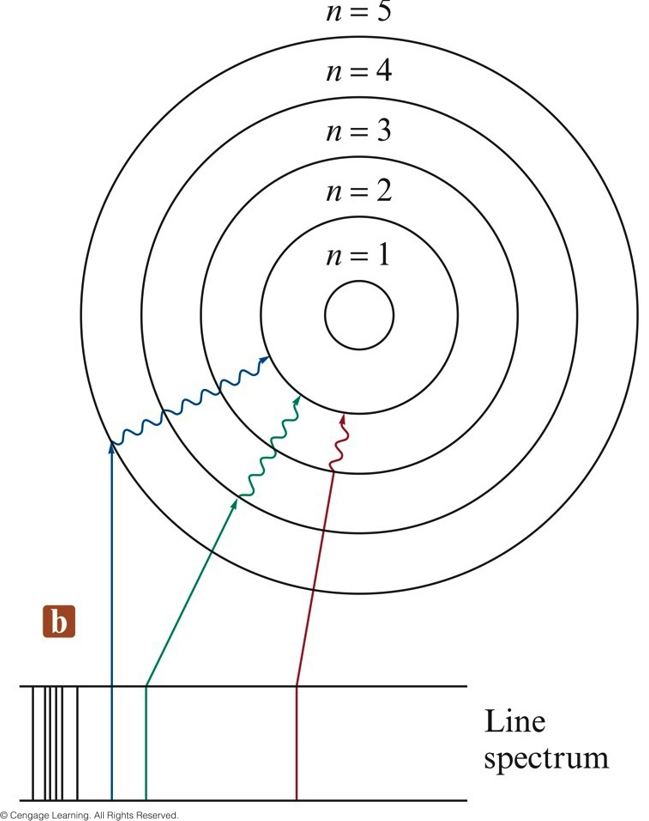
In 1913, after returning to Copenhagen, he began publishing his theory of the simplest atom, hydrogen, based on the planetary model of the atom. Bohr became convinced of its validity and spent part of 1912 at Rutherford’s laboratory. The great Danish physicist Niels Bohr (1885–1962) made immediate use of Rutherford’s planetary model of the atom. Rutherford’s Atom Model was undoubtedly a breakthrough in atomic studies.


 0 kommentar(er)
0 kommentar(er)
